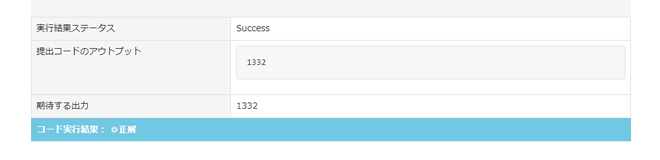
【二重ループメニュー】格子点 (paizaランク C)-解答例-PHP編

2022年7月14日

【二重ループメニュー】> 【活用編：三角形の探索】STEP: 6 格子点 (paizaランク C 相当) [難易度: 1336 ±16]

※リンク先へ移動するためには[paiza]へのログインが必要です。

問題文

x + y < 100 かつ (x ^ 3) + (y ^ 3) < 100000 が成り立つような正の整数 x , y について x × y の最大値を求めてください。

・ヒント
2 つの式を連立不等式として解きたくなりますが、x + y < 100 に注目すると、(x , y) のとりうる値は (1,1) , (1,2) , (1,98) , (2,1)... (98,1) のいずれかであり、これらは高々 98 + 97 + ... + 1 = 99 × 44 = 4356 通り（等差数列の和の公式を利用）であるため、全ての組を調べても実行時間制限に間に合います。

入力値（例）
なし

出力値（例）
条件を満たす正の整数 x , y について x × y の最大値を 1 行で出力してください。
出力の末尾には改行を入れてください。

解答例

<?php
    $max = 0;
    
    for($i = 1; $i < 99; $i++){
        for($j = 1; $j + $i < 100; $j++) {
            if($i * $i * $i + $j * $j * $j < 100000) {
                if($max < $i * $j) {
                    $max = $i * $j;
                }
            }
        }
    }
    echo $max;
?>

<?php

$max = 0;

for($i = 1; $i < 99; $i++){

for($j = 1; $j + $i < 100; $j++) {

if($i * $i * $i + $j * $j * $j < 100000) {

if($max < $i * $j) {

$max = $i * $j;

}

echo $max;

解答例

カテゴリー