【線形探索メニュー】点と点の距離 (paizaランク C)-解答例-PHP編

2022年8月11日

【線形探索メニュー】> 【特殊な探索】STEP: 5 点と点の距離 (paizaランク C 相当) [難易度: 1654 ±17]

※リンク先へ移動するためには[paiza]へのログインが必要です。

問題文

整数 n と、二次元平面上の点 1 ~ n の座標 (x_1, y_1), ... , (x_n, y_n), 整数 k が与えられます。

n 個の点 (点 n 含む) のうち、点 n とのマンハッタン距離が k 以下であるような点の数を求めてください。

なお、この問題において、2点間のマンハッタン距離とは、2点の各座標の差の絶対値の総和を指します。つまり、点 (x_i, y_i) と点 (x_j, y_j) のマンハッタン距離は、| x_i - x_j | + | y_i - y_j | です。

入力値（例）
5
-9 5
0 4
2 -6
7 -4
-3 -1
10

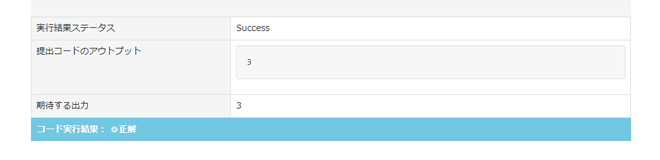
出力値（例）
3

解答例

<?php
    $n = trim(fgets(STDIN));
    
    for ($i = 0; $i < $n; $i++) {
        list($x, $y) = explode(" ", trim(fgets(STDIN)));
        $ax[] = $x;
        $ay[] = $y;
    }
    
    $k = trim(fgets(STDIN));
    
    $count = 0;
    
    for ($i = 0; $i < $n; $i++) {
        $point = abs($ax[$n - 1] - $ax[$i]) + abs($ay[$n - 1] - $ay[$i]);
        if ($point <= $k) {
            $count++;
        }
    }
    
    echo $count;
?>

<?php

$n = trim(fgets(STDIN));

for ($i = 0; $i < $n; $i++) {

list($x, $y) = explode(" ", trim(fgets(STDIN)));

$ax[] = $x;

$ay[] = $y;

}

$k = trim(fgets(STDIN));

$count = 0;

for ($i = 0; $i < $n; $i++) {

$point = abs($ax[$n - 1] - $ax[$i]) + abs($ay[$n - 1] - $ay[$i]);

if ($point <= $k) {

$count++;

}

echo $count;

解答例

カテゴリー