【DPメニュー】2項間漸化式 1 (paizaランク C)-解答例-PHP編

整数 x, d, k が与えられます。
次のように定められた数列の k 項目の値を出力してください。

(ヒント)

等差数列の公式を使えばDPを使わずとも答えを求めることができますが、練習だと思ってDPで解いてみましょう。

DPを考える際には、まず漸化式を考えるとよいです。漸化式は、数列の各項をその前の項を用いて記述した式です。問題で与えられている a_n = a_{n-1} + d という式がこの問題における漸化式となっています。

では、実際にこの問題を解いてみましょう。最終的に求めたいのは a_k です。a_1 ~ a_{k-1} がわかっているとして、a_k がどうなるかを考えてみましょう (a_1 ~ a_{k-1} が、「はじめに」の部分で述べた"部分問題"に相当しています) 。a_{k-1} がわかっているので、a_k = a_{k-1} + d とすればよいですね。今回は a_1 が x であることがわかっているので、順に a_2, a_3, a_4, ... を計算していけば a_k が求まることがわかるかと思います。

以下の疑似コードを参考にして、あなたの得意な言語で実装してみましょう。

入力値（例）
0 7 9

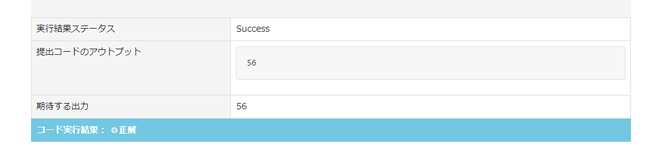
出力値（例）
56