【DPメニュー】階段の上り方 1 (paizaランク B)-解答例-PHP編

2022年8月13日

【DPメニュー】> 【階段の上り方】STEP: 1 階段の上り方 1 (paizaランク B 相当) [難易度: 1543 ±16]

※リンク先へ移動するためには[paiza]へのログインが必要です。

問題文

整数 n が与えられます。
階段を上るのに、1 歩で 1 段または 2 段を上ることができるとき、n 段の階段を上る方法は何通りあるでしょうか。

(ヒント)

これまでは問題文中に具体的な漸化式が書かれていましたが、この問題にはありません。自分で漸化式を立てる必要があります。

部分問題として、1 ~ n-1 段の階段を上る方法が何通りあるか、という問題を考えてみましょう。この部分問題の答えが求まっているとして、n 段の階段を上る方法が何通りあるかを考えてみましょう。n 段目に到達するには、n-1 段目から1段上る方法と、n-2 段目から2段上る方法の2種類が考えられます。dp[n] を n 段の階段を上る方法の数とすれば、この関係は dp[n] = dp[n-1] + dp[n-2] で表すことが出来ます。よって、0段の階段を上る方法が1通り (何もしない) であることを踏まえると、以下のようにして答えを求めることが出来ます。

入力値（例）
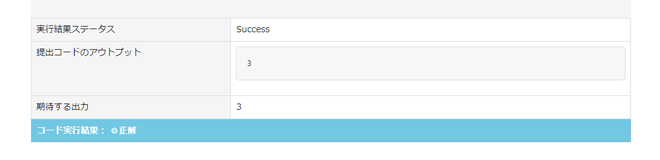
3

出力値（例）
3

解答例

<?php
    $n = trim(fgets(STDIN));
    
    $dp[0] = 1;
    
    for ($i = 1; $i <= $n; $i++) {
        $dp[$i] = 0;
        
        if ($i >= 1) {
            $dp[$i] = $dp[$i] + $dp[$i - 1];
        }
        if ($i >= 2) {
            $dp[$i] = $dp[$i] + $dp[$i - 2];
        }
    }
    echo $dp[$n];
?>

<?php

$n = trim(fgets(STDIN));

$dp[0] = 1;

for ($i = 1; $i <= $n; $i++) {

$dp[$i] = 0;

if ($i >= 1) {

$dp[$i] = $dp[$i] + $dp[$i - 1];

}

if ($i >= 2) {

$dp[$i] = $dp[$i] + $dp[$i - 2];

}

echo $dp[$n];

(ヒント)

解答例

カテゴリー