【DPメニュー】最長部分増加列 (paizaランク B)-解答例-PHP編

n 本の木が横一列に並んでいます。左から i 番目の木を木 i と呼ぶことにします。木 i の高さは a_i [cm] です。
あなたは、何本かの木を伐採することによって、残った木を左から順に見ると高さが単調増加になっているようにしたいと考えています。つまり、残った木を左から 木 k_1, 木 k_2, ... , 木 k_m とすると、a_{k_1} < a_{k_2} < ... < a_{k_m} が満たされているようにしたいです。なるべく多くの木が残るように、伐採する木を工夫して選んだとき、伐採されずに残る木の本数が最大でいくつになるか求めてください。
なお、最初から n 本の木が単調増加に並んでいる場合は、1本も伐採しなくてよいものとします。

(ヒント)

まずは問題を整理しましょう。この問題は、添字の部分列 x1 < x2 < ... < xk であって、a_x1 < a_x2 < ... < a_xk を満たしているようなもの (これを、一般に増加部分列と呼びます) のうち、k が最も大きいもの (これを、一般に最長増加部分列 (Longest Increasing Subsequence, LIS) と呼びます) を求めよという問題に言い換えることができます。

dp[k] を、最後が木 k であるような増加部分列のうち最長であるものの長さとしてみましょう。dp[1] ~ dp[k-1] が求まっているとして、dp[k] とこれらの関係はどのようになっているかを考えてみましょう。

少し考えると、1以上 k 未満の i について a_i < a_k が成り立っているとき、最後が木 i であるような増加部分列の最後に木 k をくっつけることで、新しく長さ dp[i] + 1 の増加部分列を作れることがわかります。そして、最後が木 k であるような最長増加部分列は、このようにして作られる部分列のうち最長のものであることがわかります。

これで、dp[1] ~ dp[k-1] と dp[k] の関係が明らかになりました。自信のある方は自分で漸化式を立ててみましょう。以下の疑似コードに従ってあなたの得意な言語で実装してみましょう。

dp[1] <- 1
for i = 2 to n
dp[i] <- 1 // 木 i のみからなる部分列の長さ
for j = 1 to i-1
if a[j] < a[i] then
dp[i] <- max(dp[i], dp[j]+1)
　　　// 最後が木 j であるような増加部分列の末尾に木 i をくっつける
print max({dp[1], ... ,dp[n]})

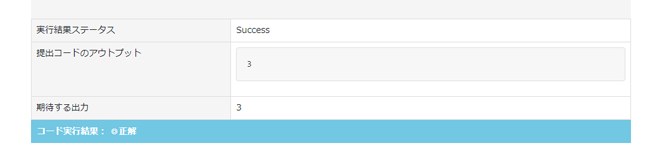
入力値（例）
5
100
102
101
91
199

出力値（例）
3